|
[拼音]:liuxing shang de fenxi
[外文]:analysis on manifolds
流形上的大范围分析与整体分析。
从局部看,微分流形与欧氏空间中某个开集同胚,因此流形上的局部分析与欧氏空间开集上的经典分析相仿。这样,所谓流形上的分析主要是指大范围分析与整体分析。这时也会呈现出与欧氏空间开集上的分析相同的现象。例如关于C∞映射的萨德定理和可微函数的惠特尼开拓定理,以及斯托克斯定理等,但更受到注意的是由流形的拓扑结构、微分结构、复结构等给分析带来的影响。
莫尔斯理论
微积分中最基本的问题是一个函数的极大与极小问题。达到极值的必要条件是一阶导数等于0。对于定义在n维流形M上的实值函数ƒ(p),p∈M,如果在坐标映射 作用下, 作用下,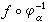 关于Rn的坐标(x1,x2,…,xn)的各个偏导数在 p点均为0,就称p为ƒ的一个临界点。它不依赖于坐标的选取。同样地,极值只能在临界点达到。但是美国数学家H.M.莫尔斯首先在1930年前后认识到这些点的数目与流形的拓扑有着密切的关系。以h(ƒ)记二阶偏导数嬠ƒ/嬠xi嬠xj构成的矩阵,若h(ƒ)在p点满秩,就称p为非退化的临界点。这时候,可以选取坐标(x1,x2,…,xn),使得p点的坐标为(0,0,…,0),而 关于Rn的坐标(x1,x2,…,xn)的各个偏导数在 p点均为0,就称p为ƒ的一个临界点。它不依赖于坐标的选取。同样地,极值只能在临界点达到。但是美国数学家H.M.莫尔斯首先在1930年前后认识到这些点的数目与流形的拓扑有着密切的关系。以h(ƒ)记二阶偏导数嬠ƒ/嬠xi嬠xj构成的矩阵,若h(ƒ)在p点满秩,就称p为非退化的临界点。这时候,可以选取坐标(x1,x2,…,xn),使得p点的坐标为(0,0,…,0),而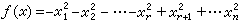 ,r就称为这个临界点的指数。r=0时ƒ达到极小;r=n时ƒ达到极大,0<r<n时ƒ不一定达到极值。这时又称p为鞍点。这些非退化的临界点均是孤立的。若ƒ 的所有临界点均非退化,就称ƒ 为莫尔斯函数。这类函数是很多的,它们按适当的拓扑在函数空间中稠密。 ,r就称为这个临界点的指数。r=0时ƒ达到极小;r=n时ƒ达到极大,0<r<n时ƒ不一定达到极值。这时又称p为鞍点。这些非退化的临界点均是孤立的。若ƒ 的所有临界点均非退化,就称ƒ 为莫尔斯函数。这类函数是很多的,它们按适当的拓扑在函数空间中稠密。
假定M是紧的微分流形,ƒ为它的一个莫尔斯函数。以μi记指数为i的临界点个数,则μi<∞。设bi为M的第i个贝蒂数(以有理数作系数的第i个同调群的维数)。那么成立莫尔斯不等式 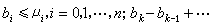 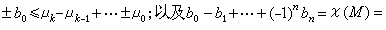 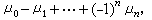 这里 ⅹ(M)为M的欧拉示性数。由这些关系式,可以从M的拓扑结构推出莫尔斯函数的极值性质。例如对于二维环面T,已知b0(T)=b2(T)=1,b1(T)=2,ⅹ(T)=0,那么环面上的莫尔斯函数的极大值点个数与极小值点个数均为1,鞍点个数为2。另一方面,若巧妙地构造莫尔斯函数,则可推出流形的拓扑结构。 这里 ⅹ(M)为M的欧拉示性数。由这些关系式,可以从M的拓扑结构推出莫尔斯函数的极值性质。例如对于二维环面T,已知b0(T)=b2(T)=1,b1(T)=2,ⅹ(T)=0,那么环面上的莫尔斯函数的极大值点个数与极小值点个数均为1,鞍点个数为2。另一方面,若巧妙地构造莫尔斯函数,则可推出流形的拓扑结构。
莫尔斯函数的临界点与流形的拓扑之间这种深刻而明确的关系使这个理论有着极为广泛的应用。R.博特的周期性定理本来就是利用莫尔斯理论证明的。S.斯梅尔及其他数学家对高维庞加莱猜想的证明和流形的分类等工作均是建立在这个理论的基础上,莫尔斯本人也曾将这个理论应用于微分几何中的雅可比场等大范围变分的研究。
这个理论已被直接推广到无限维的希尔伯特流形,这种流形与希尔伯特空间局部微分同胚。所考虑的函数必须满足弱紧致条件。
积分周期理论
流形上分析的另一重要分支,述及微分形式的积分周期,它完全反映了流形的同调特征。
如果拓扑空间X上每个局部为常数的函数总是整体为常数的话,那么X 就是连通的。于是,若记h 0(X)为局部常数的实值函数构成的向量空间,则dim h0(X)就是X 的连通分支数了。这种现象的高维推广,在1930年由法国数学家 G.-W.德·拉姆给出。由于局部常数的函数特征为 dƒ=0,因此对于微分流形M,h1(M)也将是M上的某些微分方程的解。考虑1形式 θ=Σαidxi,这里αi是M上的C∞函数。它沿着道路 у的积分成为道路у的函数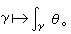 可以仿照上面一样,要求当у固定端点作小的形变时这个积分恒为常数。此时由斯托克斯定理可知dθ=0,这里d为外微分,即 可以仿照上面一样,要求当у固定端点作小的形变时这个积分恒为常数。此时由斯托克斯定理可知dθ=0,这里d为外微分,即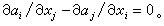 另一方面, 另一方面,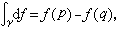 这里p,q为γ的端点,即对于形式dƒ,其积分自然地为局部常数。于是h1(M)可考虑成由局部常数的线积分与局部常数函数空间取商构成的向量空间。一般地,若φ为k阶微分形式,dφ=0,则称φ为闭的微分形式。若存在k-1阶微分形式α 使φ=dα,称φ为正合的微分形式。 这里p,q为γ的端点,即对于形式dƒ,其积分自然地为局部常数。于是h1(M)可考虑成由局部常数的线积分与局部常数函数空间取商构成的向量空间。一般地,若φ为k阶微分形式,dφ=0,则称φ为闭的微分形式。若存在k-1阶微分形式α 使φ=dα,称φ为正合的微分形式。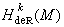 ={闭的 k阶C∞微分形式}/{正合的k阶C∞微分形式}称为M 的第k个德·拉姆上同调群。令 φ为代表德·拉姆上同调类 {φ}的 k阶闭形式,σ 为代表实可微奇异同调类{σ}的一个k循环,那么 ={闭的 k阶C∞微分形式}/{正合的k阶C∞微分形式}称为M 的第k个德·拉姆上同调群。令 φ为代表德·拉姆上同调类 {φ}的 k阶闭形式,σ 为代表实可微奇异同调类{σ}的一个k循环,那么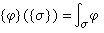 与代表元φ、σ的选取无关,定义了从 与代表元φ、σ的选取无关,定义了从 到实可微奇异同调群的对偶空间上的线性映射。德·拉姆定理肯定这个映射当M为紧微分流形时是同构,因此 到实可微奇异同调群的对偶空间上的线性映射。德·拉姆定理肯定这个映射当M为紧微分流形时是同构,因此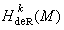 与实系数的r 阶可微奇异上同调群同构。由微分形式在一个可微循环上的积分确定的实数称作这个微分形式的周期。由斯托克斯公式可知正合微分形式的周期全为零。德·拉姆定理表明周期为零的闭形式一定正合,且若σ1,σ2,…,σt是流形M的可微k循环的任意一组基,αi为t个任意实数,那么一定存在闭的k阶C∞微分形式φ使得 与实系数的r 阶可微奇异上同调群同构。由微分形式在一个可微循环上的积分确定的实数称作这个微分形式的周期。由斯托克斯公式可知正合微分形式的周期全为零。德·拉姆定理表明周期为零的闭形式一定正合,且若σ1,σ2,…,σt是流形M的可微k循环的任意一组基,αi为t个任意实数,那么一定存在闭的k阶C∞微分形式φ使得
英国数学家W.V.D.霍奇对德·拉姆理论作出了重要改进。在霍奇理论中,一般假定流形为紧的,并具有黎曼度量。利用这个度量,构造作用在微分形式上的拉普拉斯-贝尔特拉米算子 Δ=dδ+δΔ,这里d为外微分算子,δ为d的形式共轭(按所给度量)。对于欧氏空间及其通常的平坦度量,Δ即为作用在微分形式的每个分量上的拉普拉斯算子。满足方程Δφ=0的 φ称为调和微分形式。霍奇理论肯定在每个德·拉姆上同调类中存在惟一的调和形式,也即总是存在惟一的调和形式具有预先给定的周期(见霍奇理论)。
示性类
流形上分析常与流形的度量有关,但是将受到该流形的各种示性类的限制。这些示性类虽然可以用度量的曲率矩阵来表示,但是对于不同的度量它们总在同一个上同调类内。设E)为n 维流形M上的复向量丛,Ω为E 的容许连络所对应的曲率矩阵,则混合微分形式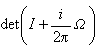 (按外乘积展开)中的2j次分量为实值闭外微分形式。它所决定的德拉姆上同调类Cj(E)与E的埃尔米特结构和连络的选取无关,称之为E 的第 j个陈类。高斯-博内定理肯定 (按外乘积展开)中的2j次分量为实值闭外微分形式。它所决定的德拉姆上同调类Cj(E)与E的埃尔米特结构和连络的选取无关,称之为E 的第 j个陈类。高斯-博内定理肯定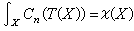 ,这里T(X)为紧复流形X的切丛。假定E 为M上以V为纤维型的l维实向量丛。令E圱C为E的复化,这是以l维复向量空间V圱C为纤维型的复向量丛。设C2j是复向量丛E圱C的第2j个陈类,则称 ,这里T(X)为紧复流形X的切丛。假定E 为M上以V为纤维型的l维实向量丛。令E圱C为E的复化,这是以l维复向量空间V圱C为纤维型的复向量丛。设C2j是复向量丛E圱C的第2j个陈类,则称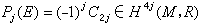 是第j个庞特里亚金类。 是第j个庞特里亚金类。
层论
复分析中的基本问题是具有给定性质的全纯函数或亚纯函数的存在与多少。问题的局部解是容易的,关键在于如何将这些局部解并接成整体解。层论正是提供了从局部分析到整体分析这个过程的有力工具。这个理论首先由法国数学家J.勒雷为研究代数拓扑而发展起来,但是最重要的应用却首先在复分析(包括复的代数几何)中。这是由于H.嘉当、J.P.塞尔、小平邦彦及D.C.斯潘塞等数学家的工作。
设F, X为二个拓扑空间,π为F到X的映射且满足下列条件: ①π连续且为局部同胚映射;
(2)对每个x∈X,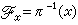 是个阿贝尔群,且群运算(α,b) 是个阿贝尔群,且群运算(α,b)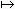 α+b关于F的拓扑是连续的,那就称F为X上的阿贝尔群层。类似地可以定义具有其他代数结构的层。在复分析中最常用的是各类函数与各类微分形式的芽层。进而设X为复流形,Uα,Uβ为x∈X的二个邻域,ƒα,ƒβ分别为Uα,Uβ上的二个Cr函数。如果在x的更小邻域 α+b关于F的拓扑是连续的,那就称F为X上的阿贝尔群层。类似地可以定义具有其他代数结构的层。在复分析中最常用的是各类函数与各类微分形式的芽层。进而设X为复流形,Uα,Uβ为x∈X的二个邻域,ƒα,ƒβ分别为Uα,Uβ上的二个Cr函数。如果在x的更小邻域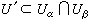 上ƒα=ƒβ,就称这二个函数等价。Cr函数的每个等价类称为x点的一个Cr函数芽。在同一点的芽按普通加法构成阿贝尔群。将X上各点的所有 Cr函数芽并在一起即得 X上的 Cr函数芽层。映射可取成将芽映到它在X的所在点。例如在x点的全纯函数芽全体记成 上ƒα=ƒβ,就称这二个函数等价。Cr函数的每个等价类称为x点的一个Cr函数芽。在同一点的芽按普通加法构成阿贝尔群。将X上各点的所有 Cr函数芽并在一起即得 X上的 Cr函数芽层。映射可取成将芽映到它在X的所在点。例如在x点的全纯函数芽全体记成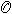 x,并在一起得到的层 x,并在一起得到的层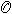 称为X上的全纯函数芽层。映射 π: 称为X上的全纯函数芽层。映射 π: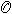 →X为 →X为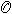 x=π-1(x)。 x=π-1(x)。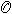 的拓扑这样定义:记ƒx为全纯函数ƒ 在x点确定的芽,那么{ƒy:y∈U,U嶅X为开集且是ƒ的定义域}构成 的拓扑这样定义:记ƒx为全纯函数ƒ 在x点确定的芽,那么{ƒy:y∈U,U嶅X为开集且是ƒ的定义域}构成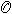 的开集基。这时π为局部同胚且群运算连续。其他种类的函数芽层的拓扑,甚至各类微分形式芽层的拓扑都可类似地定义。 的开集基。这时π为局部同胚且群运算连续。其他种类的函数芽层的拓扑,甚至各类微分形式芽层的拓扑都可类似地定义。
将普通上同调群的系数代之以层的元素,即得取值在某个层内的上同调群。hq(X,F)就是取值在F内的第q个上同调群。若F为常数函数芽层,它就是普通的上同调群,如果F为其他函数类的芽层,那么h 0(X,F)就代表定义在整个X 上的这类函数的多少。它往往从高阶上同调群的信息中算得。
例如设{pi}是非紧黎曼面S上的一个离散点集,要求找一个亚纯函数ƒ在点pi具有给定的主部。假定{Uα}为M的一个开覆盖,φα为Uα上的亚纯函数且在{pi}∩Uα具有给定的主部(这是容易做到的局部问题)。于是在Uα∩Uβ上φα-φβ=ƒαβ就是全纯函数。这些函数{ƒαβ}代表了h1(M,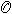 )中的一个元素。在h1(M, )中的一个元素。在h1(M,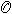 )=0时,就会在Uα(或更小的开集)上存在全纯函数ψα,使得在Uα∩Uβ上ψα-ψβ=ƒαβ,从而φα-ψα=φβ-ψβ。这样{φα-ψα}就是定义在整个S上又满足要求的亚纯函数。所以,具有给定性质的解是否存在就变成某个上同调群为零。所幸总有h1(S, )=0时,就会在Uα(或更小的开集)上存在全纯函数ψα,使得在Uα∩Uβ上ψα-ψβ=ƒαβ,从而φα-ψα=φβ-ψβ。这样{φα-ψα}就是定义在整个S上又满足要求的亚纯函数。所以,具有给定性质的解是否存在就变成某个上同调群为零。所幸总有h1(S,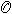 )=0。在高维,这类问题称为第一库辛问题。当X 为施泰因流形时,h1(X, )=0。在高维,这类问题称为第一库辛问题。当X 为施泰因流形时,h1(X,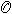 )=0,因此这个问题有解。类似地寻求具有给定零点集的全纯函数的问题称为第二库辛问题。除了X 的施泰因性质外尚需其他条件,例如h2(X, Z)=0,才能使这个问题有解(见多复变函数论)。 )=0,因此这个问题有解。类似地寻求具有给定零点集的全纯函数的问题称为第二库辛问题。除了X 的施泰因性质外尚需其他条件,例如h2(X, Z)=0,才能使这个问题有解(见多复变函数论)。
对于n维复流形X,当F为X 上的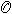 模层时, 又称F为解析层。记p个层 模层时, 又称F为解析层。记p个层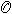 的直和为 的直和为 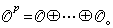 它也是层。若每个x∈X,存在邻域U及整数p、q使得 它也是层。若每个x∈X,存在邻域U及整数p、q使得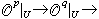 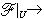 0是U上的层同态正合序列,就称F为凝聚解析层。 0是U上的层同态正合序列,就称F为凝聚解析层。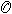 p本身即为凝聚解析层。这时候对一切q>n成立hq(X,F)=0。如果X为施泰因流形,则嘉当定理B 意味着对一切q>0,hq(X,F)=0。如果X为紧复流形,那么对一切q≥0,hq(X,F)为有限维的。 p本身即为凝聚解析层。这时候对一切q>n成立hq(X,F)=0。如果X为施泰因流形,则嘉当定理B 意味着对一切q>0,hq(X,F)=0。如果X为紧复流形,那么对一切q≥0,hq(X,F)为有限维的。
对于紧黎曼面S,dim h1(S,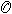 )=g 即为S的亏格数。S上的一个因子D是指一个有限形式和 )=g 即为S的亏格数。S上的一个因子D是指一个有限形式和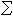 nipi,pi∈S,ni为整数。以vi(ƒ)记亚纯函数ƒ在pi的洛朗展开式的首项指数,那么对于任意i成立vi+ni≥0的亚纯函数形成向量空间l(D)。微分形式hdz亚纯是指h为亚纯函数。对任何i成立vi(h)≥ni的亚纯微分形式全体记作i(D),那么黎曼-罗赫定理肯定 nipi,pi∈S,ni为整数。以vi(ƒ)记亚纯函数ƒ在pi的洛朗展开式的首项指数,那么对于任意i成立vi+ni≥0的亚纯函数形成向量空间l(D)。微分形式hdz亚纯是指h为亚纯函数。对任何i成立vi(h)≥ni的亚纯微分形式全体记作i(D),那么黎曼-罗赫定理肯定 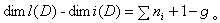 每个因子D 对应一个全纯线丛λ(D),使本来为亚纯的对象在λ(D)内成为全纯的元素。对于全纯向量丛π:E→M,以Ω(E)记E 的全纯截面芽层(E在M的开集U上的全纯截面是指全纯映射F:U→E,且π。F 为恒同映射)。利用塞尔对偶定理,上述公式左边可写成 每个因子D 对应一个全纯线丛λ(D),使本来为亚纯的对象在λ(D)内成为全纯的元素。对于全纯向量丛π:E→M,以Ω(E)记E 的全纯截面芽层(E在M的开集U上的全纯截面是指全纯映射F:U→E,且π。F 为恒同映射)。利用塞尔对偶定理,上述公式左边可写成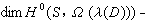  这种上同调维数的交错和形式。J.P.塞尔在证明了他的对偶定理并重新解释了黎曼-罗赫定理后猜想:当M是代数流形时, 这种上同调维数的交错和形式。J.P.塞尔在证明了他的对偶定理并重新解释了黎曼-罗赫定理后猜想:当M是代数流形时,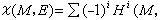 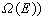 一定可以写成一个只包含M的陈类及E 的陈类的多项式在M的基本同调类上的值。这猜想立刻被德国数学家F.希策布鲁赫在1954年证明: 一定可以写成一个只包含M的陈类及E 的陈类的多项式在M的基本同调类上的值。这猜想立刻被德国数学家F.希策布鲁赫在1954年证明: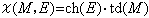 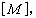 式中的 式中的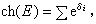 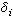 由以E的陈类Cj为系数的形式多项式 由以E的陈类Cj为系数的形式多项式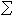 Cjxj的分解式所决定,即 Cjxj的分解式所决定,即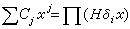 , 习惯上称ch(E)为E的陈特征,又称 , 习惯上称ch(E)为E的陈特征,又称 为E的托德类,若T(M)表示M的切丛,则 为E的托德类,若T(M)表示M的切丛,则 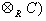 称为M的托德类。 称为M的托德类。
黎曼-罗赫-希策布鲁赫公式又为A.格罗腾迪克推广。他利用复流形上凝聚解析层的性质,将ⅹ(M,E)的计算看成一个关于全纯映射的公式。如果M、N是两个代数流形,ƒ∶M→N是个全纯映射,则同时也由ƒ建立了M和N 的所谓黎曼-罗赫群之间的关系。对应的公式就是格罗腾迪克-黎曼-罗赫定理。如果N退化为一点,ƒ就为常值映射,公式就变成希策布鲁赫公式。这个观点所包含的许多想法使之成为代数K 理论以及拓扑K 理论的出发点。
希策布鲁赫公式的另一推广就是阿蒂亚-辛格指标定理,由这个定理可推出希策布鲁赫公式对任何紧复流形成立。
微分算子
流形上分析的许多问题常与作用在流形上的微分算子有关。例如霍奇理论中出现的 Δ就是二阶椭圆型算子,这里主要考虑的是任意阶椭圆型算子。
设M为紧的可定向n维光滑流形。E、F为M上的二个光滑复向量丛。Г(E)、Г(F)分别记E、F 的光滑截面空间。线性微分算子P∶P(E)→Г(F局部地可以用偏导数的矩阵来表示。设T*(M)为M 的余切丛,S(M)为T*(M中的单位球面丛(关于某个黎曼度量)。设π∶S(M)→M 为射影,那么有一个与P 有关的向量丛同态σ(P):π*E →π*F,称为P的象征。当σ(P)是一个向量丛同构时,称P为椭圆型的(见流形上的偏微分算子)。椭圆型算子的基本性质是它的核 KerP(P 的零空间)和余核Coker P =Г(F )/PГ(E )都是有限维的。其维数之差у(P)=dim kerP-dim CokerP 称为P的解析指标。如果P*:Г(F)→Г(E)为P的形式共轭算子(关于E、F、M的度量),那么P*也是椭圆型的,并且CokerP≌kerP*,因此у(P)=dimkerP-dimkerP*。у(P)在P 形变时不变,因此韦夸和盖尔范德猜想у(P)可以用拓扑不变量来表达。这个猜想为M.F.阿蒂亚和I.M.辛格所证实。若以 ch(P)记由E、F、σ(P)所决定的上同调环h*(X,Q)中的一个元素,td(M)为M 的托德类,那么称
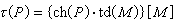
为P的拓扑指标,阿蒂亚-辛格指标定理表明
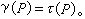
将这个定理应用于P =d+δ,这里d为普通的外微分算子,δ 是d 的形式共轭,那就得到霍奇理论的一个结论:调和微分形式空间维数的交错和等于流形的欧拉示性数,以及希策布鲁赫的符号差定理。设X 为紧复流形,再将这个定理应用于作用在X 上的全纯向量丛上的算子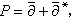 这里扺*为扺的形式共轭,那就会表明黎曼-罗赫-希策布鲁赫定理对一切紧复流形成立。由于许多分析问题与椭圆型算子有关,因此这个定理还有许多应用。 这里扺*为扺的形式共轭,那就会表明黎曼-罗赫-希策布鲁赫定理对一切紧复流形成立。由于许多分析问题与椭圆型算子有关,因此这个定理还有许多应用。
阿蒂亚-辛格指标定理可推广到更一般的椭圆复形
它们的象征在 S(M)上正合。由此可得一般椭圆复形的莱夫谢茨不动点公式。应用于德·拉姆复形,即得本来的莱夫谢茨不动点公式,这个定理也可推广到有边界的紧流形的椭圆型边值问题上,还可用于流形的变换群的研究。
在非紧复流形上扺 算子是经常出现的。它与霍奇理论与超定微分方程组理论密切相关,是高维复分析研究中的一个基本工具。
- 参考书目
- B.Booss and D.D.Bleecker,Topology and Analy-sis;The Atiyah-Singer Index Formula and Gɑnge-Theoretic Physics,China Academic Publishers, Springer-Verlag, Beijing, 1985.
- F.Hirzebruch,Topological Methods in Algebraic Geometry,Springer-Verlag, Berlin, 1978.
- D.W.Kahn,Introduction to Global Analysis,Academic Press, New York, 1980.
- J.W.Milnor,characteristic Classes, Ann. Math.St.,No.76, Princeton Univ. Press, Princeton,1974.
- F.W.Warner,Foundations of Differentiable Manifolds and Lie Groups,China Academic Press, Beijing, 1983.
|
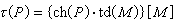
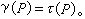
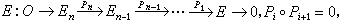

 作用下,
作用下,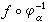 关于Rn的坐标(x1,x2,…,xn)的各个偏导数在 p点均为0,就称p为ƒ的一个临界点。它不依赖于坐标的选取。同样地,极值只能在临界点达到。但是美国数学家H.M.莫尔斯首先在1930年前后认识到这些点的数目与流形的拓扑有着密切的关系。以h(ƒ)记二阶偏导数嬠ƒ/嬠xi嬠xj构成的矩阵,若h(ƒ)在p点满秩,就称p为非退化的临界点。这时候,可以选取坐标(x1,x2,…,xn),使得p点的坐标为(0,0,…,0),而
关于Rn的坐标(x1,x2,…,xn)的各个偏导数在 p点均为0,就称p为ƒ的一个临界点。它不依赖于坐标的选取。同样地,极值只能在临界点达到。但是美国数学家H.M.莫尔斯首先在1930年前后认识到这些点的数目与流形的拓扑有着密切的关系。以h(ƒ)记二阶偏导数嬠ƒ/嬠xi嬠xj构成的矩阵,若h(ƒ)在p点满秩,就称p为非退化的临界点。这时候,可以选取坐标(x1,x2,…,xn),使得p点的坐标为(0,0,…,0),而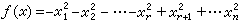 ,r就称为这个临界点的指数。r=0时ƒ达到极小;r=n时ƒ达到极大,0<r<n时ƒ不一定达到极值。这时又称p为鞍点。这些非退化的临界点均是孤立的。若ƒ 的所有临界点均非退化,就称ƒ 为莫尔斯函数。这类函数是很多的,它们按适当的拓扑在函数空间中稠密。
,r就称为这个临界点的指数。r=0时ƒ达到极小;r=n时ƒ达到极大,0<r<n时ƒ不一定达到极值。这时又称p为鞍点。这些非退化的临界点均是孤立的。若ƒ 的所有临界点均非退化,就称ƒ 为莫尔斯函数。这类函数是很多的,它们按适当的拓扑在函数空间中稠密。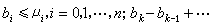
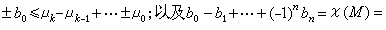
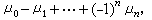 这里 ⅹ(M)为M的欧拉示性数。由这些关系式,可以从M的拓扑结构推出莫尔斯函数的极值性质。例如对于二维环面T,已知b0(T)=b2(T)=1,b1(T)=2,ⅹ(T)=0,那么环面上的莫尔斯函数的极大值点个数与极小值点个数均为1,鞍点个数为2。另一方面,若巧妙地构造莫尔斯函数,则可推出流形的拓扑结构。
这里 ⅹ(M)为M的欧拉示性数。由这些关系式,可以从M的拓扑结构推出莫尔斯函数的极值性质。例如对于二维环面T,已知b0(T)=b2(T)=1,b1(T)=2,ⅹ(T)=0,那么环面上的莫尔斯函数的极大值点个数与极小值点个数均为1,鞍点个数为2。另一方面,若巧妙地构造莫尔斯函数,则可推出流形的拓扑结构。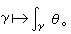 可以仿照上面一样,要求当у固定端点作小的形变时这个积分恒为常数。此时由斯托克斯定理可知dθ=0,这里d为外微分,即
可以仿照上面一样,要求当у固定端点作小的形变时这个积分恒为常数。此时由斯托克斯定理可知dθ=0,这里d为外微分,即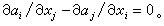 另一方面,
另一方面,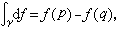 这里p,q为γ的端点,即对于形式dƒ,其积分自然地为局部常数。于是h1(M)可考虑成由局部常数的线积分与局部常数函数空间取商构成的向量空间。一般地,若φ为k阶微分形式,dφ=0,则称φ为闭的微分形式。若存在k-1阶微分形式α 使φ=dα,称φ为正合的微分形式。
这里p,q为γ的端点,即对于形式dƒ,其积分自然地为局部常数。于是h1(M)可考虑成由局部常数的线积分与局部常数函数空间取商构成的向量空间。一般地,若φ为k阶微分形式,dφ=0,则称φ为闭的微分形式。若存在k-1阶微分形式α 使φ=dα,称φ为正合的微分形式。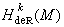 ={闭的 k阶C∞微分形式}/{正合的k阶C∞微分形式}称为M 的第k个德·拉姆上同调群。令 φ为代表德·拉姆上同调类 {φ}的 k阶闭形式,σ 为代表实可微奇异同调类{σ}的一个k循环,那么
={闭的 k阶C∞微分形式}/{正合的k阶C∞微分形式}称为M 的第k个德·拉姆上同调群。令 φ为代表德·拉姆上同调类 {φ}的 k阶闭形式,σ 为代表实可微奇异同调类{σ}的一个k循环,那么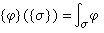 与代表元φ、σ的选取无关,定义了从
与代表元φ、σ的选取无关,定义了从 到实可微奇异同调群的对偶空间上的线性映射。德·拉姆定理肯定这个映射当M为紧微分流形时是同构,因此
到实可微奇异同调群的对偶空间上的线性映射。德·拉姆定理肯定这个映射当M为紧微分流形时是同构,因此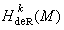 与实系数的r 阶可微奇异上同调群同构。由微分形式在一个可微循环上的积分确定的实数称作这个微分形式的周期。由斯托克斯公式可知正合微分形式的周期全为零。德·拉姆定理表明周期为零的闭形式一定正合,且若σ1,σ2,…,σt是流形M的可微k循环的任意一组基,αi为t个任意实数,那么一定存在闭的k阶C∞微分形式φ使得
与实系数的r 阶可微奇异上同调群同构。由微分形式在一个可微循环上的积分确定的实数称作这个微分形式的周期。由斯托克斯公式可知正合微分形式的周期全为零。德·拉姆定理表明周期为零的闭形式一定正合,且若σ1,σ2,…,σt是流形M的可微k循环的任意一组基,αi为t个任意实数,那么一定存在闭的k阶C∞微分形式φ使得
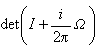 (按外乘积展开)中的2j次分量为实值闭外微分形式。它所决定的德拉姆上同调类Cj(E)与E的埃尔米特结构和连络的选取无关,称之为E 的第 j个陈类。高斯-博内定理肯定
(按外乘积展开)中的2j次分量为实值闭外微分形式。它所决定的德拉姆上同调类Cj(E)与E的埃尔米特结构和连络的选取无关,称之为E 的第 j个陈类。高斯-博内定理肯定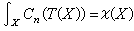 ,这里T(X)为紧复流形X的切丛。假定E 为M上以V为纤维型的l维实向量丛。令E圱C为E的复化,这是以l维复向量空间V圱C为纤维型的复向量丛。设C2j是复向量丛E圱C的第2j个陈类,则称
,这里T(X)为紧复流形X的切丛。假定E 为M上以V为纤维型的l维实向量丛。令E圱C为E的复化,这是以l维复向量空间V圱C为纤维型的复向量丛。设C2j是复向量丛E圱C的第2j个陈类,则称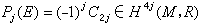 是第j个庞特里亚金类。
是第j个庞特里亚金类。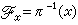 是个阿贝尔群,且群运算(α,b)
是个阿贝尔群,且群运算(α,b)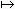 α+b关于F的拓扑是连续的,那就称F为X上的阿贝尔群层。类似地可以定义具有其他代数结构的层。在复分析中最常用的是各类函数与各类微分形式的芽层。进而设X为复流形,Uα,Uβ为x∈X的二个邻域,ƒα,ƒβ分别为Uα,Uβ上的二个Cr函数。如果在x的更小邻域
α+b关于F的拓扑是连续的,那就称F为X上的阿贝尔群层。类似地可以定义具有其他代数结构的层。在复分析中最常用的是各类函数与各类微分形式的芽层。进而设X为复流形,Uα,Uβ为x∈X的二个邻域,ƒα,ƒβ分别为Uα,Uβ上的二个Cr函数。如果在x的更小邻域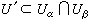 上ƒα=ƒβ,就称这二个函数等价。Cr函数的每个等价类称为x点的一个Cr函数芽。在同一点的芽按普通加法构成阿贝尔群。将X上各点的所有 Cr函数芽并在一起即得 X上的 Cr函数芽层。映射可取成将芽映到它在X的所在点。例如在x点的全纯函数芽全体记成
上ƒα=ƒβ,就称这二个函数等价。Cr函数的每个等价类称为x点的一个Cr函数芽。在同一点的芽按普通加法构成阿贝尔群。将X上各点的所有 Cr函数芽并在一起即得 X上的 Cr函数芽层。映射可取成将芽映到它在X的所在点。例如在x点的全纯函数芽全体记成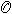 x,并在一起得到的层
x,并在一起得到的层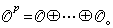 它也是层。若每个x∈X,存在邻域U及整数p、q使得
它也是层。若每个x∈X,存在邻域U及整数p、q使得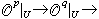
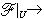 0是U上的层同态正合序列,就称F为凝聚解析层。
0是U上的层同态正合序列,就称F为凝聚解析层。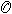 p本身即为凝聚解析层。这时候对一切q>n成立hq(X,F)=0。如果X为施泰因流形,则嘉当定理B 意味着对一切q>0,hq(X,F)=0。如果X为紧复流形,那么对一切q≥0,hq(X,F)为有限维的。
p本身即为凝聚解析层。这时候对一切q>n成立hq(X,F)=0。如果X为施泰因流形,则嘉当定理B 意味着对一切q>0,hq(X,F)=0。如果X为紧复流形,那么对一切q≥0,hq(X,F)为有限维的。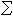 nipi,pi∈S,ni为整数。以vi(ƒ)记亚纯函数ƒ在pi的洛朗展开式的首项指数,那么对于任意i成立vi+ni≥0的亚纯函数形成向量空间l(D)。微分形式hdz亚纯是指h为亚纯函数。对任何i成立vi(h)≥ni的亚纯微分形式全体记作i(D),那么黎曼-罗赫定理肯定
nipi,pi∈S,ni为整数。以vi(ƒ)记亚纯函数ƒ在pi的洛朗展开式的首项指数,那么对于任意i成立vi+ni≥0的亚纯函数形成向量空间l(D)。微分形式hdz亚纯是指h为亚纯函数。对任何i成立vi(h)≥ni的亚纯微分形式全体记作i(D),那么黎曼-罗赫定理肯定 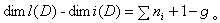 每个因子D 对应一个全纯线丛λ(D),使本来为亚纯的对象在λ(D)内成为全纯的元素。对于全纯向量丛π:E→M,以Ω(E)记E 的全纯截面芽层(E在M的开集U上的全纯截面是指全纯映射F:U→E,且π。F 为恒同映射)。利用塞尔对偶定理,上述公式左边可写成
每个因子D 对应一个全纯线丛λ(D),使本来为亚纯的对象在λ(D)内成为全纯的元素。对于全纯向量丛π:E→M,以Ω(E)记E 的全纯截面芽层(E在M的开集U上的全纯截面是指全纯映射F:U→E,且π。F 为恒同映射)。利用塞尔对偶定理,上述公式左边可写成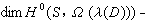
 这种上同调维数的交错和形式。J.P.塞尔在证明了他的对偶定理并重新解释了黎曼-罗赫定理后猜想:当M是代数流形时,
这种上同调维数的交错和形式。J.P.塞尔在证明了他的对偶定理并重新解释了黎曼-罗赫定理后猜想:当M是代数流形时,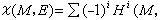
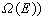 一定可以写成一个只包含M的陈类及E 的陈类的多项式在M的基本同调类上的值。这猜想立刻被德国数学家F.希策布鲁赫在1954年证明:
一定可以写成一个只包含M的陈类及E 的陈类的多项式在M的基本同调类上的值。这猜想立刻被德国数学家F.希策布鲁赫在1954年证明: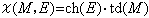
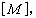 式中的
式中的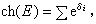
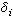 由以E的陈类Cj为系数的形式多项式
由以E的陈类Cj为系数的形式多项式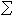 Cjxj的分解式所决定,即
Cjxj的分解式所决定,即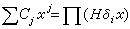 , 习惯上称ch(E)为E的陈特征,又称
, 习惯上称ch(E)为E的陈特征,又称 为E的托德类,若T(M)表示M的切丛,则
为E的托德类,若T(M)表示M的切丛,则
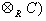 称为M的托德类。
称为M的托德类。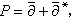 这里扺*为扺的形式共轭,那就会表明黎曼-罗赫-希策布鲁赫定理对一切紧复流形成立。由于许多分析问题与椭圆型算子有关,因此这个定理还有许多应用。
这里扺*为扺的形式共轭,那就会表明黎曼-罗赫-希策布鲁赫定理对一切紧复流形成立。由于许多分析问题与椭圆型算子有关,因此这个定理还有许多应用。






