流形上的控制理论

[拼音]：liuxing shang de kongzhi lilun

[外文]：control theory on manifolds

建立在微分流形基础上的、研究控制系统的运动和特性的理论。微分流形是通常意义下光滑曲面概念的推广。在微分流形上的每一点周围都可建立一个局部的欧几里得坐标系，但不一定能在整个流形上建立统一的欧几里得坐标。欧几里得空间只是微分流形的一个特例。不少实际系统的状态变量的取值范围都可以看成为微分流形。流形上的控制理论比传统的控制理论更具有一般性。研究流形上的控制系统的主要数学工具是微分几何。对流形上的控制理论的研究始于20世纪70年代初，它的出现为非线性系统理论的研究开辟了新的途径。由于问题本身的困难性和数学方法的复杂性，这一理论中成熟的结果还不多，它尚处于形成和发展的阶段。

在流形上的控制理论中，系统的数学模型的一般形式为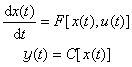

式中t表示时间；x(t)，u(t)和y(t)分别为系统的状态向量、控制向量和输出向量（见状态空间法）。xt是微分流形M上的点即x∈M，u和y均在欧几里得空间中取值。F[·，u]是M上的可微向量场,C是可微函数，dx/dt是定义在流形上的微商。在实际应用中，研究得较多的是比较特殊的一类系统：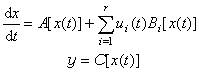

式中A和B_i，i＝1,2,…,r,都是M上的可微向量场，这里提到的两种系统模型分别对应于通常的非线性控制系统和双线性系统。

流形上的控制理论对一些有关的基本问题已取得一些结果，其中包括能控性和能达性、不变分布、线性化。

能控性和能达性

状态_z∈M是由状态x ∈M 能达的，规定为存在容许控制u(t)，使得在有限时间内u(t)可以把状态_z引导到状态x。用Ω(x)表示由状态x能达的状态的集合，则当 Ω(x)＝M时系统的状态x称为能控。如果每个状态x ∈M都是能控的,则称系统是能控的。能控性涉及系统在流形上的整体性质,是一个很困难的问题,尚未完满解决。如果Ω(x)包含M的一个非空开子集，状态 x就称为能达的,这是比能控性弱一些的概念。关于能达性的一些重要的结果是由H.J.萨斯曼和V.J.尤杰维茨利用李代数方法得到的。