消费函数
|
[拼音]:xiaofei hanshu [外文]:consumption function 消费与其决定因素之间的函数关系。决定消费水平的因素很多,如收入、财产、利率、收入分布等。其中收入是最根本的因素。因此,消费函数实质上是指消费与收入之间的函数关系。 消费函数这一概念最先由英国经济学家J.M.凯恩斯提出。他在《就业、利息和货币通论》(1936)一书中提出:总消费是总收入的函数。这一思想用线性函数形式表示为: 第二次世界大战以后,西方经济学家对消费函数进行了较深入的研究,提出了若干新的假说及相应的函数式。其中函数形式比较简单而内容大体符合实际的消费函数是: 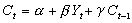
式中C t表示t期消费,Y t表示t期收入,C t-1表示上期(t-1期)消费; α,β,γ为参数。这一消费函数的最后一项可以解释为消费的惯性影响,也可以解释为持久收入的影响。因为应用递推关系可将上面的消费函数改写为: 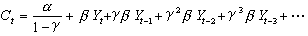
此式表明,消费是过去历年收入的函数。 消费函数主要应用于宏观经济分析之中。西方的宏观经济模型通常把消费作为其核心方程之一。中国学术界从80年代开始消费函数的理论和实证研究,已将消费函数纳入中国宏观经济模型中。 |
热门点击
最近更新

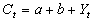 ,式中C表示总消费,Y表示总收入,下标t表示时期;a、b为参数。参数b称为边际消费倾向,其值介于0与1之间。凯恩斯的这个消费函数仅仅以收入来解释消费,被称为绝对收入假说。这一假说过于简单粗略,用于预测时误差较大。
,式中C表示总消费,Y表示总收入,下标t表示时期;a、b为参数。参数b称为边际消费倾向,其值介于0与1之间。凯恩斯的这个消费函数仅仅以收入来解释消费,被称为绝对收入假说。这一假说过于简单粗略,用于预测时误差较大。


















