假设检验
|
[拼音]:jiashe jianyan [外文]:hypothesis testing 又称统计假设检验,是一种基本的统计推断形式,也是数理统计学的一个重要的分支。“假设”是指关于总体分布的一项命题。例如,一群人的身高服从正态分布N(μ,σ2),则命题“均值μ≤1.70(米)”是一个假设。又如,有一批产品,其废品率为p,则“p≤0.03”这个命题也是一个假设。假设是否正确,要用从总体中抽出的样本进行检验,与此有关的理论和方法,构成假设检验的内容。 设A是关于总体分布的一项命题,所有使命题A成立的总体分布构成一个集合h0,称为原假设(常简称假设)。使命题A不成立的所有总体分布构成另一个集合h1,称为备择假设。如果h0可以通过有限个实参数来描述,则称为参数假设,否则称为非参数假设(见非参数统计)。如果h0(或h1)只包含一个分布,则称原假设(或备择假设)为简单假设,否则为复合假设。对一个假设h0进行检验,就是要制定一个规则,使得有了样本以后,根据这规则可以决定是接受它(承认命题A正确),还是拒绝它(否认命题A正确)。这样,所有可能的样本所组成的空间(称样本空间)被划分为两部分HA和HR(HA的补集),当样本x∈HA时,接受假设h0;当x∈HR时,拒绝h0。集合HR常称为检?a href='http://www.b15k.com/baike/222/323577.html' target='_blank' style='color:#136ec2'>榈木芫颍琀A称为接受域。因此选定一个检验法,也就是选定一个拒绝域,故常把检验法本身与拒绝域HR等同起来。 显著性检验有时,根据一定的理论或经验,认为某一假设h0成立,例如,通常有理由认为特定的一群人的身高服从正态分布。当收集了一定数据后,可以评价实际数据与理论假设h0之间的偏离,如果偏离达到了“显著”的程度就拒绝h0,这样的检验方法称为显著性检验。怎样去规定什么时候偏离达到显著的程度?通常是指定一个很小的正数α(如0.05,0.01),使当h0正确时,它被拒绝的概率不超过α,称α为显著性水平。这种假设检验问题的特点是不考虑备择假设,就上例而言,问题可以说成是考虑实验数据与理论之间拟合的程度如何,故此时又称为拟合优度检验。拟合优度检验是一类重要的显著性检验。 K.皮尔森在1900年提出的ⅹ2检验是一个重要的拟合优度检验。设原假设h0是:“总体分布等于某个已知的分布函数F(x)”。把(-∞,∞)分为若干个两两无公共点的区间I1,I2,…,Ik,对任一个区间
皮尔森证明了:若 奈曼-皮尔森理论J.奈曼与 E.S.皮尔森合作,从1928年开始,对假设检验提出了一项系统的理论。他们认为,在检验一个假设h0时可能犯两类错误:第一类错误是真实情况为h0成立(即θ∈嘷0),但判断h0不成立,犯了“以真为假”的错误。第二类错误是h0实际不成立(即θ∈嘷1),但判断它成立,犯了“以假为真”的错误(见表 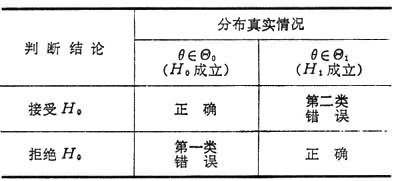
)。这里嘷0,嘷1分别是使假设h0成立或不成立的θ的集合,显然嘷=嘷0+嘷1。当θ∈嘷0,样本X(即X1,X2,…,Xn组成的向量)∈HR,其概率Pθ(X∈HR)就是犯第一类错误的概率α;当θ∈嘷1,样本X∈HA,其概率
中的 p0、p1、α、β根据需要选定。这种图形清楚地描述了犯两类错误的概率。 优良性准则基于奈曼-皮尔森理论及统计决策理论,可以提出一些准则,来比较为检验同一假设而提出的各种检验。较重要的准则有: 一致最大功效(UMP)准则欲检验h0:θ∈嘷0,h1:θ∈嘷1;当给定检验水平α后,在所有满足 无偏性准则要求检验在备择假设h1成立时作出正确判断的概率不小于检验水平α,这就是说在h0不成立时拒绝h0的概率要不小于在h0成立时拒绝h0的概率,这种性质称为无偏性,具有这种性质的检验称为无偏检验。显然,如果在无偏检验中存在一致最大功效检验就称为一致最大功效无偏检验(简称UMPU检验)。UMP检验不存在时,仍可能有UMPU检验存在。例如正态总体中方差未知时,为检验均值μ=μ0的t检验就是UMPU检验,但不是UMP检验。 因为假设检验在统计决策理论中是一种特殊的统计决策问题,两类错误影响可用特殊损失来表示。例如选取特殊的损失函数,使正确判断时损失为零,错判时损失为1。它就可归结为犯第一类错误的概率α和犯第二类错误的概率β。这同用功效函数Pθ(X∈HR)来叙述是一致的。因此把统计决策理论中容许性、同变性、贝叶斯决策、最小化最大等概念引进来,而得到容许检验、同变检验、贝叶斯检验和最小化最大检验。在同变检验限制下,又可以建立一致最大功效同变检验的概念。这些准则又可作为假设检验的优良性准则,从而扩大了假设检验的内容。 寻求在一定准则下的最优检验是很困难的,何况这种最优检验有时并不存在。于是提出了若干依据直观的推理法,其中最重要的是似然比法。 似然比检验运用与最大似然估计(见点估计)类似的原理,可得到似然比检验法。设样本X的分布密度即似然函数为l(尣,θ),θ∈嘷,欲检验的假设为h0:θ∈嘷0,称 
为似然比。显然0≤ 用似然比法导出的重要检验有: U 检验若总体遵从正态分布N(μ,σ2),其中σ已知,X=(X1,X2,…,Xn)是从总体中抽取的简单随机样本,记
的检验,其中μ0是给定的常数,α为检验的水平,uα为标准正态分布的上α分位数。上述检验称为U 检验。 t检验若总体服从正态分布N(μ,σ2),但σ未知,记
,其中tα为自由度为n-1的t分布的上α分位数。这些检验称为t检验。 F 检验若X=(X1,X2,…,
,其中Fα为自由度为(n1-1,n2-1)的F分布的上α分位数。这些检验称为F检验,在方差分析中有广泛的应用。
|

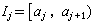 ,以vj记大小为n的样本X1,X2,…,Xn中落在Ij内的个数,称为区间Ij的观测频数,另外,求出Ij的理论频数
,以vj记大小为n的样本X1,X2,…,Xn中落在Ij内的个数,称为区间Ij的观测频数,另外,求出Ij的理论频数 (对j=1,2,…,k都这样做),再算出由下式定义的ⅹ2统计量
(对j=1,2,…,k都这样做),再算出由下式定义的ⅹ2统计量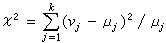 ,
, 对j=1,2,…,k,则当n→∞时,ⅹ2的极限分布是自由度为k-1的ⅹ2分布。于是在样本大小n相当大时,从ⅹ2分布表可查得ⅹ2分布的上α分位数(见概率分布)ⅹ
对j=1,2,…,k,则当n→∞时,ⅹ2的极限分布是自由度为k-1的ⅹ2分布。于是在样本大小n相当大时,从ⅹ2分布表可查得ⅹ2分布的上α分位数(见概率分布)ⅹ (k-1)。由此即得检验水平为α的拒绝域:{ⅹ2≥ⅹα(k-1)}。如果原假设h 0为:总体服从分布族{Fθ,θ∈嘷},式中θ为未知参数,嘷为θ的所有可能取值的集合(称参数空间),也可得到类似的拒绝域,只要在计算理论频数vj时,将所包含的未知参数θ用适当的点估计代替,即可计算 ⅹ2统计量。但此时极限分布的自由度为 k-Л-1,式中Л为θ中的独立参数的个数。柯尔莫哥洛夫检验(见非参数统计)也是一个重要的拟合优度检验方法。
(k-1)。由此即得检验水平为α的拒绝域:{ⅹ2≥ⅹα(k-1)}。如果原假设h 0为:总体服从分布族{Fθ,θ∈嘷},式中θ为未知参数,嘷为θ的所有可能取值的集合(称参数空间),也可得到类似的拒绝域,只要在计算理论频数vj时,将所包含的未知参数θ用适当的点估计代替,即可计算 ⅹ2统计量。但此时极限分布的自由度为 k-Л-1,式中Л为θ中的独立参数的个数。柯尔莫哥洛夫检验(见非参数统计)也是一个重要的拟合优度检验方法。 就是犯第二类错误的概率β。通常人们不希望轻易拒绝h0,例如工厂的产品一般是合格的,出厂进行抽样检查时不希望轻易地被认为不合格,于是在限定犯第一类错误的概率不超过某个指定值α(称为检验水平)的条件下,寻求犯第二类错误的概率尽可能小的检验方法。为了描述检验的好坏,称θ的函数Pθ(X∈HR)为检验的功效函数。例如上述产品检验的例子中,所采用的检验可以是:当样品中的废品个数超过一定限度时,认为该批产品不合格,否则就认为合格。这个检验的功效函数有图示的形状,图
就是犯第二类错误的概率β。通常人们不希望轻易拒绝h0,例如工厂的产品一般是合格的,出厂进行抽样检查时不希望轻易地被认为不合格,于是在限定犯第一类错误的概率不超过某个指定值α(称为检验水平)的条件下,寻求犯第二类错误的概率尽可能小的检验方法。为了描述检验的好坏,称θ的函数Pθ(X∈HR)为检验的功效函数。例如上述产品检验的例子中,所采用的检验可以是:当样品中的废品个数超过一定限度时,认为该批产品不合格,否则就认为合格。这个检验的功效函数有图示的形状,图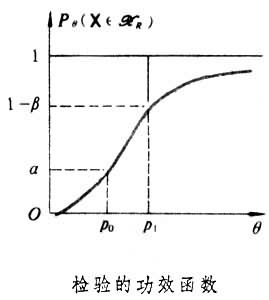

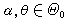 的可供选择的检验HR中,是否有一个最好的,亦即:是否存在拒绝域H
的可供选择的检验HR中,是否有一个最好的,亦即:是否存在拒绝域H ,使得对于所有θ∈嘷1及一切检验水平为α的H
,使得对于所有θ∈嘷1及一切检验水平为α的H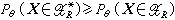 。若这样的检验存在,则称HR为检验水平α的一致最大功效检验,简称UMP检验。奈曼与皮尔森在1933年提出了著名的奈曼-皮尔森引理。这是对简单假设寻求UMP检验的一个构造性的结果,即此时似然比检验就是UMP检验。对某些复合假设也找到了 UMP检验,但并不是所有情况都存在 UMP检验。因此有必要在对检验作某些限制下寻找最大功效检验或建立另外一些优良性准则。
。若这样的检验存在,则称HR为检验水平α的一致最大功效检验,简称UMP检验。奈曼与皮尔森在1933年提出了著名的奈曼-皮尔森引理。这是对简单假设寻求UMP检验的一个构造性的结果,即此时似然比检验就是UMP检验。对某些复合假设也找到了 UMP检验,但并不是所有情况都存在 UMP检验。因此有必要在对检验作某些限制下寻找最大功效检验或建立另外一些优良性准则。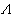 (尣)≤1,当
(尣)≤1,当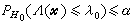 。然而,在一般情况下,寻求
。然而,在一般情况下,寻求 (尣的精确分布并不容易。1938年S.S.威尔克斯证明了:在相当广泛的条件下,-2ln
(尣的精确分布并不容易。1938年S.S.威尔克斯证明了:在相当广泛的条件下,-2ln ,则
,则 遵从标准正态分布N(0,1),于是可考虑对μ的以下几种假设
遵从标准正态分布N(0,1),于是可考虑对μ的以下几种假设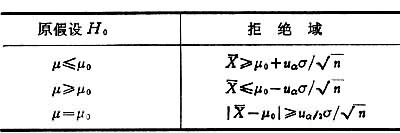
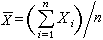 ,
, ,则t=
,则t=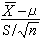 遵从自由度为n-1的t分布,可对μ有以下的水平为α的检验
遵从自由度为n-1的t分布,可对μ有以下的水平为α的检验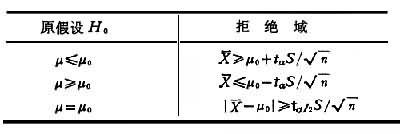
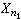 )及Y=(Y1,Y2,…,
)及Y=(Y1,Y2,…,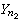 )分别为来自正态总体N(μ1,σ娝)及N(μ2,σ娤)的简单随机样本,记
)分别为来自正态总体N(μ1,σ娝)及N(μ2,σ娤)的简单随机样本,记  ,
,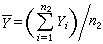 ,
,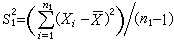 ,
, ,则
,则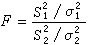 遵从自由度为n1-1,n2-1的F分布,对比较σ娝与σ娤的假设有以下的水平为α的检验
遵从自由度为n1-1,n2-1的F分布,对比较σ娝与σ娤的假设有以下的水平为α的检验



















