构造逻辑
|
[拼音]:gouzao luoji [外文]:constructive logic 一种非经典的逻辑系统。它主要由对数学持直觉主义、构造主义或致力于构造性数学研究和发展的数学家和逻辑学家建立和使用。在数理逻辑和数学基础中,“构造性”一词有几种不同的理解并在几种不同的意义下使用,其共同之处在于它们都满足下列构造性要求: (1)对存在命题ヨxAx的一个证明是构造性的,如果从这个证明能找到(构造出)一个特殊的对象x,它满足A; (2)不能无条件地使用排中律。按照构造性观点,对于p∨塡p,只有在有一个方法能判明p与塡p中哪一个是真的情况下,才能承认它是真的,而不承认任一命题非真即假。按照这些构造性观点建立的逻辑就是构造逻辑。 从构造性观点看不可接受的证明的例子,如定理: 存在两个无理数a和b,使得a b 是有理数。该定理的一个非构造性证明是: 说明经典逻辑和构造逻辑之间的对照的一个简单例子,是考虑所谓肯定的蕴涵演算,这个演算只有一个逻辑常项,即蕴涵词,它有两个公理和一条推理规则: A1.A→(B→A); A2.(A→(B→C))→((A→B)→(A→C)); 规则E.如果A并且A→B,那么B。从构造性数学观点看,这个系统是足够的。但是,它并没有在下述意义上刻划出作为一个真值函项的蕴涵,即A→B是真的当且仅当 A假或者B真。例如,[((A→B)→A)→A](即Peirce律)是一个重言式,但它在这个系统中是不能证明的。如果在该系统中增加以下两个关于否定的公理,能得到就蕴涵和否定而言的构造命题演算。这两个关于否定的公理为: A3.(A→塡A)→塡A; A4.塡A→(A→B)。但要得到经典命题演算,则需要在上面系统中再增一条公理 A5.塡塡A→A。和排中律一样,该公理在构造逻辑中也是不成立的。 在构造逻辑中,对于逻辑联结词塡(非)、∧(并且)、∨(或者)、→(如果,则,)和量词ヨx(存在一个 x,有一个x)、凬 x(所有x)的理解如下: (1)对A∧B的一个证明由A的一个证明和B的一个证明一起构成; (2)对 A∨B的一个证明由特别指定的A的一个证明或者由特别指定的 B的一个证明构成; (3)对A→B的一个证明由一个构造c构成,构造c可把A的任一证明转换成B的一个证明,即构造 c具有如果d是A的一个证明,把c与d结合起来就产生 B的一个证明这种性质; (4)以符号⊥表示一个不可证的命题,对塡A的一个证明由一个构造c构成,构造c把对A的任一证明转换成对⊥的一个证明; (5)如果个体变元x取值于某个“基本的”个体域D,则对凬xA(x)的一个证明由一个构造c组成,当把构造c应用于域D中的任一个体d时,就产生对A(d)的一个证明c(d); (6)如果个体变元x取值于某个“基本的”个体域D,则对ヨ xA(x)的一个证明由一个构造 c和域D中的一个个体d构成,并且构造 c是对A(d)的一个证明。 在构造逻辑中,各个联结词和量词都是彼此独立、不能相互定义的。 从20世纪30年代以来,构造逻辑已建立了多个形式系统。其中,K.哥德尔在1958年构作的系统为: (1)A,A→B崊B; (2)A→B,B→C崊A→C; (3)A∨A→A,A→A∧A; (4)A→A∨B,A∧B→A; (5)A∨B→B∨A,A∧→B∧A; (6)A→B崊C∨A→C∨B; (7)A∧B→C崊A→(B→C) (8)A→(B→C)崊A∧B→C; (9)⊥→A; (10)B→A(x)崊B→凬xA(x)(x在 B中不自由出现); 凬xA(x)→A(t)(t对于A中的x自由); A(t)→ヨxA(x)(t对于A中的x自由); A(x)→B崊ヨxA(x)→B(x在 B中不自由出现),其中的崊为元数学符号。 |

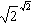 或者是有理数或者是无理数,假若
或者是有理数或者是无理数,假若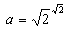 ,b=匇,则a和b是无理数且
,b=匇,则a和b是无理数且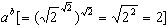 是有理数,故所取的a和b满足定理。于是定理得证。从经典的逻辑和数学的观点看,该证明是无懈可击的,因而该定理确是成立的。但从构造性的观点来看,这个证明仅是根据排中律肯定
是有理数,故所取的a和b满足定理。于是定理得证。从经典的逻辑和数学的观点看,该证明是无懈可击的,因而该定理确是成立的。但从构造性的观点来看,这个证明仅是根据排中律肯定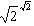 或者是有理数或者是无理数而作出的,但没有任何方法指明
或者是有理数或者是无理数而作出的,但没有任何方法指明


















