洛伦兹力
|
[拼音]:luolunzili [外文]:Lorentz force 运动的带电粒子同时受到的电场和磁场的作用力,为荷兰物理学家H.A.洛伦兹首先提出,故得名。若粒子所带的电荷为q,在电场E和磁场B中粒子的运动速度为v,则洛伦兹力F可表示为: F=q(E+v×B), 式?a href='http://www.b15k.com/baike/222/320239.html' target='_blank' style='color:#136ec2'>杏叶说谝幌钗绾?I>q所受的电场力;第二项为该运动电荷所受的磁场力。洛伦兹力的力密度f可写成: f=ρeE+J×B, 式中右端第一项为单位体积物质中的电荷所受的电场力,其中ρe为电荷密度;第二项为上述电荷运动形成的电流所受的磁场力(简称磁场力),其中J=ρev为电流密度。 磁场力垂直于电流方向和磁场方向并符合右手螺旋定则(图1)。 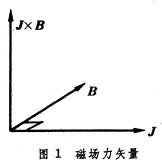
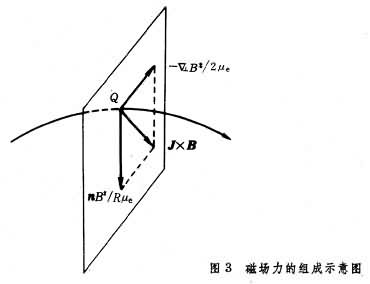
电动机的转动就是磁场力作用的结果。等离子体或其他导电流体就是通过洛伦兹力同电磁场之间进行动量和能量交换的。若忽略电场随时间的变化,则磁场力可用下述的应力表示法加以说明。如图2所示,磁应力由两部分组成:一是同流体压强性质类似的磁压B2/2μe,其中μe为磁导率;另一是沿磁力线切线方向的张力B2/μe。因此,磁力线好似绷紧的弦,而磁力线之间有相互排斥力。在任一点Q,单位体积流体所受的磁场力J×B是两个力的矢量和(图3):一是由于弯曲磁力线中的张力导致的磁向心力nB2/Rμe,其中n和R分别为磁力线在Q点的主法线单位矢量和曲率半径;另一是垂直于磁场方向的负磁压梯度-墷寑B2/2μe。故磁场力可表示为: J×B=nB2/Rμe-墷寑B2/2μe。 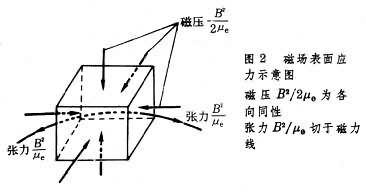
 |
热门点击
最近更新




















