电磁场的边值问题
|
[拼音]:diancichang de bianzhi wenti [外文]:boundary-value problems of electromagnetic field 由区域内的已知场源和边界上的物理状况,通过麦克斯韦方程组求解区域内电磁场的问题。 静场情形对于静电场,基本方程归结为静电势嗞(r)的泊松方程
式中ρ(r)是已知的电荷密度,r是位矢,ε是介电常数,即真空介电常数ε0乘以相对介电常数εr。如区域T内无场源ρ(r),方程(1)化为拉普拉斯方程墷2嗞=0。静电场的边值问题就是泊松方程或拉普拉斯方程的边值问题,边值条件视情况而异。如果是导体面,往往是给定电势的第一类边值问题(狄利克雷问题)或给定其上的总电荷,后者相当于给定电位移D的法向分量 对于随时间变化的电磁场,常将B和E用矢量势A(r,t)和标量势嗞(r,t)表出
A和嗞是不惟一的,下列替换并不影响式(2)
其中f(r,t)是任取的标量函数(见电磁势)。替换式(3)叫规范变换。如果选取洛伦兹规范
这是非齐次波动方程,电磁场的变化以电磁波或电磁振荡的形式进行,波速(相速,见波)为 电磁场方程是线性的,可将电磁场分解为各种频率的单色(单频率)场的线性叠加即傅里叶级数或傅里叶积分,从而只需着重研究单色场
式中ω为圆频率,即频率乘以2π。从以上两式可得到亥姆霍兹方程 墷2E+k2E=0, 墷2B+k2B=0, (7) 其中 方程(7)是矢量方程。如果用笛卡儿坐标,则E(r)和B(r)的各分量分别满足标量亥姆霍兹方程 墷2u+k2u=0。 (8) 这样,电磁场的边值问题就是矢量或标量亥姆霍兹方程的边值问题。对于波导或谐振腔,如果把器壁看作是理想导体,则边界条件是E的切向分量为零,B的法向分量为零。对于电磁波的衍射问题,在瑞利-索末菲理论中,边界条件是入射在孔径上的场。 解的唯一性数学上可以证明,泊松方程(1)或拉普拉斯方程在前述边界条件下的解是惟一的,电势有时可以相差一无关紧要的常数。如果场源局限于有限区域而求解区域伸展至无限远,边界条件还要求 拉普拉斯方程在零边界条件下的惟一解是零解。亥姆霍兹方程有所不同,存在一系列数kn(n=1,2,3,…)使得方程 只要k不等于λn,亥姆霍兹方程在边界条件 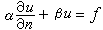
(α,β,f 已知)下的解是惟一的。对于伸展至无限远的区域,还要加上索末菲辐射条件 常用的求解方法有镜像法。还有分离变量法,即对于某个正交坐标系来说,在边界形状比较规则的情况下,把偏微分方程分解成常微分方程,从而求出用本征函数展开成无穷级数的解。还有格林函数法,即在一定条件下,寻找附加了边界条件的微分算子的反算子的积分核,进而求得积分形式解析解。此外,还有将某些边界条件较复杂的平面标量场转化为边界形状较简单的平面标量场的保角变换法等。以上这些方法都受边界形状和场域介质的限制,用它们可以求得解析解的电磁场边值问题很有限,在很多情况下需要依靠数值解法。数值解法很多,如差分法;在一定边值条件下求某泛函极值的里兹法;以及由里兹法和伽辽金法发展而来的有限元法等。
|

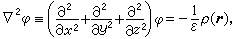 (1)
(1)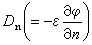 的积分值
的积分值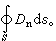 。如果边界面是两电介质1、2的分界面,且分界面上无自由电荷,则边界条件为电位移D的法向分量连续D1n=D2n,和电场强度E的切向分量连续E1t=E2t。在大多数情况下,后一条件表示电势连续嗞1=嗞2。对于静磁情况,在引入磁矢势后,可得到矢势的矢量式泊松方程。在相应的边界条件下,即可定出矢势的值。
。如果边界面是两电介质1、2的分界面,且分界面上无自由电荷,则边界条件为电位移D的法向分量连续D1n=D2n,和电场强度E的切向分量连续E1t=E2t。在大多数情况下,后一条件表示电势连续嗞1=嗞2。对于静磁情况,在引入磁矢势后,可得到矢势的矢量式泊松方程。在相应的边界条件下,即可定出矢势的值。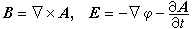 。 (2)
。 (2) (3)
(3)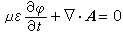 ,其中μ为磁导率,则在不导电媒质中A和嗞分别满足达朗伯方程
,其中μ为磁导率,则在不导电媒质中A和嗞分别满足达朗伯方程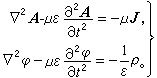 (4)
(4)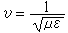 ,电流密度J)(r,t)和电荷密度ρ(r,t)是激励源。如区域中无激励源,可直接用E和B来描述电磁场,得齐次波动方程p">
,电流密度J)(r,t)和电荷密度ρ(r,t)是激励源。如区域中无激励源,可直接用E和B来描述电磁场,得齐次波动方程p">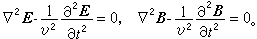 (5)
(5)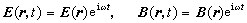 , (6)
, (6)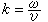 为波矢值。
为波矢值。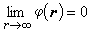 。
。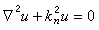 在零边界条件下有非零解un,这些kn和un称为该边值问题的本征值λn和本征函数,相应的电磁振荡称为本征模式。一般的振荡是这些本征模式的线性叠加,叠加系数根据初始条件决定;在实际的应用中,则往往用适当的激励方式,使得只有特定模式被激励。
在零边界条件下有非零解un,这些kn和un称为该边值问题的本征值λn和本征函数,相应的电磁振荡称为本征模式。一般的振荡是这些本征模式的线性叠加,叠加系数根据初始条件决定;在实际的应用中,则往往用适当的激励方式,使得只有特定模式被激励。