偏微分方程的基本解
|
[拼音]：pianweifen fangcheng de jibenjie [外文]：fundamental solution of partial differential equation 偏微分方程的一种具有特定奇异性的解，由它可以构造出一般的解。例如对于二维和三维拉普拉斯方程的基本解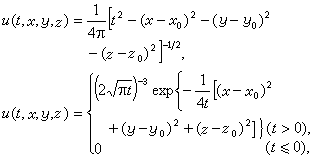 
也有类似的作用（见双曲型偏微分方程、抛物型偏微分方程）。 J.（-S.）阿达马对二阶线性偏微分方程 
在解析系数与非抛物（即det(αij)≠0）的条件，作出了以下形状的基本解
式中 广义函数是研究基本解的有力工具。线性偏微分算子 l的基本解即适合下式的广义函数E（p，p0）：l(E)=δ(p-p0)，δ是狄喇克函数。当l为常系数算子时，E(p，p0)=E(p-p0)。 若能作出E，则l(u)=ƒ将有解u=E*ƒ：l(E*ƒ)=l(E)*ƒ=δ*ƒ=ƒ。 对常系数偏微分算子l，利用傅里叶变换可形式地作出基本解 对变系数线性偏微分算子，则有必要将基本解概念推广为拟基本解。在构造拟基本解并研究其性质与应用方面，拟微分算子与傅里叶积分算子有着根本的作用。 |
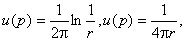可用来构造出该方程的“通解”以及格林函数（见椭圆型偏微分方程）。对于三维的波动方程和热传导方程，它的基本解
，
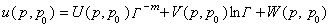U、V、W是
，
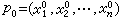的解析函数，Г是 p与p0在度量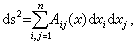
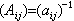下的测地距离的平方，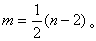
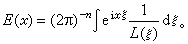这里根本的困难是l(ξ)的零点将使该积分发散。20世纪50年代中期，L.赫尔曼德尔、B.马尔格朗热与L.埃伦普雷斯独立克服了这个困难，证明了常系数线性偏微分算子基本解的存在。这是偏微分方程论的重大进展。
热门点击
最近更新